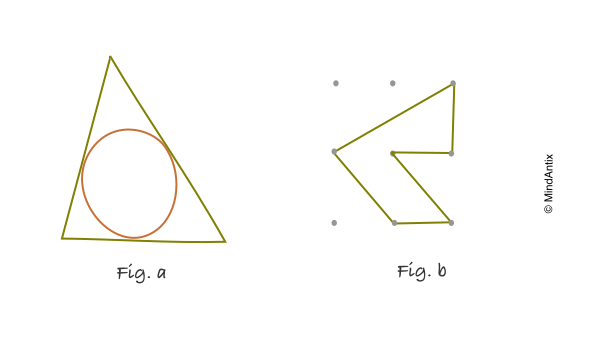In a study by the US Department of Education, 81% of 4th graders reported having a positive attitude towards mathematics but that number drops significantly to 35% for 8th graders. Somehow, in the span of four years, children lose their interest in the subject, and as a result their performance declines. Professor Eric Mann, believes that “keeping students interested and engaged in mathematics by recognizing and valuing their mathematical creativity may reverse this tendency.”
In fact, research has shown that creativity can actually help students acquire content knowledge. But, how can we encourage creativity in mathematics, a subject usually considered linear and inflexible? A few people have come up with ways to twist math problems to make them more creative and fun. So, here are three simple ways to add more creativity in mathematics.
Problem Finding
Problem finding, or problem posing, in any domain is considered to be an important and integral aspect of creativity. For this activity, students are asked to come up with as many different problems as they can with a given situation. One example that Harpen and colleagues used to evaluate creativity is:
In the picture above (Fig. a), there is a triangle and its inscribed circle. Make up as many problems as you can that are related to this picture.
Most students were able to come up with problems involving Lengths (“If the triangle is a right triangle, the hypotenuse is 2, another angle is 60o, find the radius of the circle”) or Areas (“Given the radius of the circle r, find out the minimum are of the triangle”). Creative students were able to pose questions from different fields of mathematics including less obvious ones like probability (“If you are to drop something to the circle, what is the probability of it falling into the triangle?”).
Divergent Thinking
Mathematical problems with many possible solutions can help build divergent thinking skills. Exploring multiple solutions forces students to look beyond the obvious and . One such problem posed by Haylock is:
Given a nine-dot centimeter-square draw as many shapes as possible with an area of 2cm2, by joining up the dots with straight lines.
Most children come up with the easiest solution of drawing a rectangle 2cm x 1cm, but finding other kinds of shapes gets harder. One highly creative solution shown in the picture above (Fig. b) uses two new ideas – connecting non-adjacent dots and using an internal angle of 315o.
Overcoming Fixation
A key aspect of creativity is to break free from routine patterns of thinking (flexible thinking). By forcing students to drop their established mindsets helps them in examining a problem from different perspectives and arriving at better solutions. In the same study, Haylock gave students a series of questions in which the students are asked to find two numbers given their sum and difference. The first few example use only positive integers which sets the student’s mindset to expect solutions that use only positive whole numbers. Then the students are asked:
Find two numbers where the sum is 9 and the difference is 2.
A surprisingly large number of students assert that this is not possible. The more creative students were able to remove the self-imposed constraint of using only whole numbers and get to the right solution (5.5 and 3.5).