In the early 1860s, when Leo Tolstoy was teaching writing to children of Russian peasants, he hit upon an interesting way to bring more creativity into the exercise. He asked his students to write a story on the proverb, “He eats with your spoon and then puts your eyes out with the handle.” The result of his exercise surprised even him.
After some initial hesitation, his students approached the challenge with an unexpected enthusiasm and produced a much better composition than the one Tolstoy had himself written. Tolstoy commented on the quality of his students’ work in an article with, “Every unprejudiced man with any feeling for art and nationality, on reading this first page written by me, and the following pages of the story written by the scholars themselves, will distinguish this page from all the others, like a fly in milk, it is so artificial, so false, and written in such a wretched style.”
While Tolstoy was simply trying to motivate his students to write with more vigor and authenticity, he accidently introduced his students to a key creative thinking skill – analogical reasoning.
Analogical reasoning is the ability to find relational similarity between two situations or phenomena. Robert and Michele Root-Bernstein in their book, Sparks of Genius, consider analogical reasoning to lie at “the heart of what it means to think creatively” and a skill that many scientists rate as the most important one to possess.
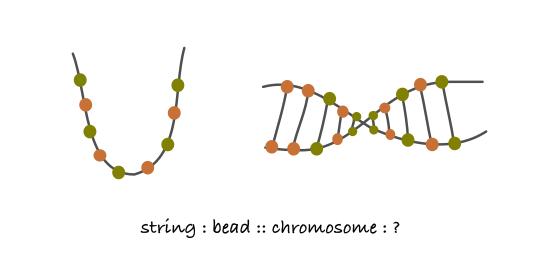
In fact, several discoveries in science can be traced back to finding the right analogy. For instance, early geneticists likened genes to beads on a string to help them understand how traits are passed along. While this simple analogy couldn’t explain everything, it did suggest possible mechanisms for inherited traits. Making analogies is a fundamental way of thinking applicable not just in science, but in almost every field like mathematics, religion and literature. Robert Frost’s metaphor of life to a journey in “The Road Not Taken” is especially powerful because of the unique associations it invokes each time.
While it’s clear that analogical thinking plays an important role in creative thinking, what exactly does it involve? Underlying analogical thinking are three mental processes – Retrieval (with a current topic in working memory, a person may be reminded of an analogous situation in long-term memory), Mapping (aligning the two situations on the relational structure and projecting inferences), and Evaluation (judging the analogy and inferences).
The MindAntix brainteaser, Proverbial Tales, inspired by Tolstoy’s challenge to his students, aims to strengthen the mental processes used in analogical reasoning. Using proverbs from different cultures, users have to construct an original story that reflects the meaning of the proverb, forcing them to go through the different stages of retrieval, mapping and evaluation.
As Robert and Michele Root-Bernstein point out, “There is so much to be learned by analogizing that we must not neglect to learn how. Like every other tool for thinking, the capacity within ourselves and our children ought to be nurtured, exercised, trained.”